dB是通信领域最常用的测量单位之一。dB的数学定义如下。它只是一个对数比例的数字。
dB = 10*Log10(P)
这样的好处是,对于高功率,小数点前的所有零或低功率,小数点后的所有零都会使计算变得困难。为方便起见,采用了单元的dB和dBm系统。
通信领域经常使用Log进行转换,为什么需要使用log进行转换呢? LOG被视为一个神奇的镜头,使小东西变大,大东西变小,如下图所示。
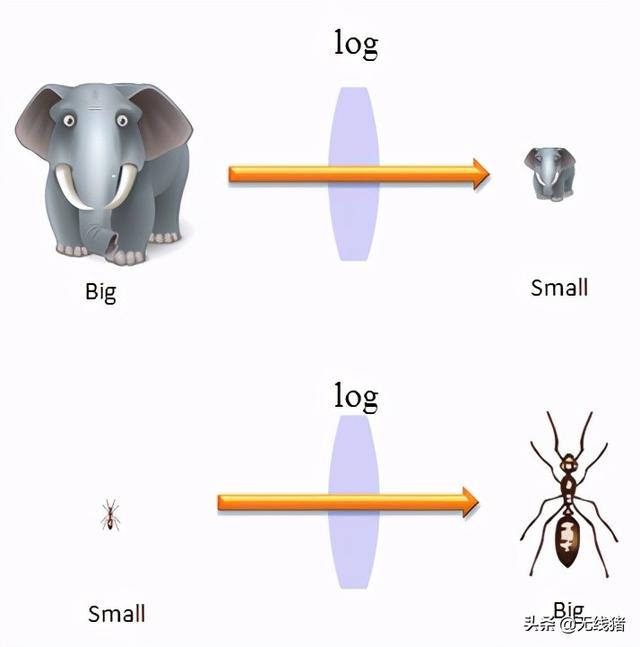
接下来的问题是“为什么需要这种神奇的镜头?”。这个问题的答案是,可视化一组同时具有非常小的值和较大值的数据。举个例子,如下所示,您可以看到整个范围内非常平滑的曲线。但是如果你放大了图的底部,它是波动的,如图的底部所示。然而,如果我们像在上图中那样以线性比例绘制图形,则不会注意到这种波动。

但是,如果以log比例函数绘制此数据。你会注意到之前没有注意到波动的区域被放大了,如(b),(c)所示。如果将图(a)-线性比例与(b)进行比较,会注意到(a)中的小值如何在(b)中放大,以及(a)中的大值如何在(b)中缩小。通过这种方法,log函数可以同时显示小数域和大数域的细节。

所以,在许多情况下,我们用分贝标度来表示一个比率。
dB = 10Log10(P/Reference)
根据它所代表的比率,我们用各种下标来表示dB,如下所示。如:dBm、dBc、dBi等。
dBm表示测量功率与1 mW的比值,即相对于1 mW的测量功率。
dBc表示特定频率点的测量功率与中心频率的功率之比。
dBi表示某一方向(辐射功率最强的方向)的辐射功率与假想各向同性辐射功率之比。在天线中经常使用。
下面给出了一些dB的例子。
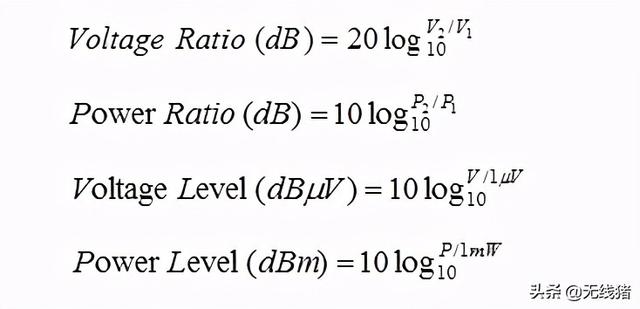
例如,放大器增益是一个单位较小的值,即放大器增益是输出功率与输入功率之比:
Pout/Pin = Gain
Gain in dB = 10*log(Pout/Pin)

所以,dB是两种不同功率水平的相对度量。3dB是两倍(或一半),6dB是四倍,10dB是十倍,依此类推。
因此,我可以说放大器有20分贝的增益,或者我有6分贝的总馈线电缆损耗。我不能说,我的放大器提供30分贝的输出功率,因为你必须说明你引用的是什么,这就是下标的来源。dB本身不是一个绝对数,而是一个比率。
dBm是用来测量幂的(对数)单位。因为dB是一个功率比,所以dBm是通过形成你想要表达的功率与参考功率的比值来定义的,对于dBm来说是1mw。正式地说:
功率单位:dBm=10*log10(Power/1mW)
对于放大器,绝对功率的公共参考单位是dBm,0dBm等于1毫瓦。

因此,输出功率为50dBm的放大器输出100瓦。它有多少收益完全是另一回事。
下表显示了预先计算的W、dBW、dBm值。也可以根据需要创建自己的表。













