R是一款统计计算编程语言,你可以在通用公共许可(GPL)规则下从互联网获取它。也就是说,你可以免费获取它、发布它,甚至拿它来卖钱,只要获取者与你有相同的权利,并且可以免费获得源代码。R可以在微软公司的Windows XP以及之后的版本中使用,在UNIX,Linux以及苹果公司的Macintosh OS X系统中也可以使用。
R提供了统计计算以及绘图的环境。事实上,R是一款完整的编程语言,尽管这一点在本书中鲜有提及。本书中,我们主要学习一些基本的概念,并且研究一些有指导性的例子。
R可以在某个统计计算结果的基础上再进行扩展计算。此外,R的数据可视化系统既允许我们使用诸如plot(x,y)这样的简单命令来进行绘图,也提供了对图形输出更好的控制。正因为R是一款编程语言,所以R非常灵活。其他一些统计软件,提供了更好的交互以及菜单表格类的选项接口,但是通常这样用户友好的界面反而会限制使用者进一步探索。尽管一些基本的统计只需要一些固定的计算过程,但是对于一个稍微复杂的数据进行建模,就需要一些特别设定的计算,而R的灵活性在这时就会成为显著的优势。
R之所以被称为“R”,其实是一个互联网式的幽默。也许你知道C语言(C语言之所以被称为C也是有一段故事的)。受到这种命名方式的启发,Bechker和Chambers在20世纪80年代早期为他们新发明的语言起名为S。这种语言后来被发展成一个商用的版本S-PLUS,并被全世界各地的统计学家广为使用。新西兰奥克兰大学的Ross Ihaka和Robert Gentleman为了教学目的,写了一个S的简化版。这两位先生的名字都以R开头,好吧,还有什么理由拒绝以R作为这个语言的名字呢?
在1995年,Martin Maechler劝说Ross和Robert在GPL规则下公开他们R语言的源代码。这与当时风行一时的Linux系统开源运动不谋而合。R很快给那些需要在Linux上进行统计计算的人带去了福音。很快,交流故障与讨论R发展的邮件列表就被建立起来。
初始步骤开始运行R是很简单的,但方法取决于你的操作平台。你可以从系统菜单启动,双击图标或在系统命令行中输入命令"R"。这将产生一个控制台窗口,或在当前终端窗口启动一个交互式程序。在这两种情形下,R都通过问答模式工作,即你输入命令行并按下Enter键,然后程序运行,输出相关结果,继续要求更多的输入。当R在准备输入状态时,它显示的提示符是一个">"符号。R也可以作为纯文本应用程序或批处理模式来应用,但针对本章的目的,我将假设你处于一个图形工作站上。
如果你不仅安装了ISwR包,而且也加载到当前搜索路径,那么只要你把书中所写的例子完全复制,它们就都应该能够运行。通过在命令提示符下输入

完成这一步。这里你不需要理解命令是如何处理的。2.1.5小节将给出解释。
为了看一下R能做什么,先试着输入下述命令行:
这个命令抽取1 000个服从正态分布的随机数(rnorm=random normal),并在一个弹出式窗口中绘图。图1.1是在Windows系统下的输出结果。

当然,此处你不需要猜测如何用特定的方法得到这个结果。选择这个例子是因为它可以展示活动中的用户界面的几个组成部分。在命令继续之前,有必要通过几个简单的例子介绍一些概念和惯例。
在Windows下,图形窗口设置键盘焦点在当前点上。点击控制台使其接受更多的命令。
1.1 大型计算器R中最简单的任务可能就是输入一个算术表达式并得到结果。(下面第2行是从机器上得到的结果。)

所以机器知道2加2等于4。当然,它也知道如何做其他的常规运算。比如,如何计算e-2:

结果前面的[1]是R输出数字和向量的方式的一部分。这里它没有什么用处,但在输出较长的向量时它就有用了。括号中的数字是那一行第1个数字的序号,考虑从一个正态分布中产生15个随机数的例子:

比如说,[6]在这里表示0.079 769 77是向量中的第6个元素。(出于排版的原因,本书采用的是缩短了的行宽。如果你在自己的机器上试一下,你将看到每一行输出的是6个数字而不是5个,数字本身也会不同,因为它们是随机产生的)。
1.2 赋值即使只是一个计算器,你也会很快发现为了避免将计算中间结果一遍又一遍重复地输入,你需要某种方法来储存中间结果。像其他计算机语言一样,R也有符号变量,即可以用来代表数值的名称。要给变量x赋值2,你可以输入:

字符<和-应该理解成一个符号。箭头指向的是被赋值的变量,它被称为赋值运算符。运算符中间的空格通常被R所忽视,但是注意到在<-之间增加一个空格会将其含义改变为“小于”号后面跟着“负号”(反之,当比较一个变量跟一个负数时,删除空格会引起意想不到的后果)。
这里没有立即可见的结果,但从现在开始,x的值是2并将用于后续的算术表达式中。

在R中,变量名可以自由选取。它可以由字母、数字和点号构成。然而,有一个限制是不能以数字开头,数字后也不能紧跟点号。点号开头的变量名是特殊的,应尽量避免。一个典型的变量名可以是height.1yr,可能用来描述1岁儿童的身高。变量名区分大小写,WT和 wt指的是不同的变量名。
有些变量名已经被系统使用。因此如果将它们用于其他地方,将导致混淆。最坏的情形是一些单字母变量名,如c、q、t、C、D、F、I和T,但也有其他的,比如diff、df和pt等。这些大多是函数,被用作变量名通常也不会引起太大麻烦。但是,F和T是FALSE和TRUE的标准简写,如果你重新定义,它们将失去原意。
1.3 向量运算你不可能对单个数字做太多统计!但是,你会看到很多数据,比如说从一组病人中获得的数据。R的强大功能之一就是把整个数据向量作为一个单一对象来处理。一个数据向量仅是数字的排列,一个向量可以通过如下方式构造:

结构c(…)用来构造向量。数字是编造的,但可能用来表示一组正常男性的体重(以kg为单位)。
这既不是R中输入向量的唯一方法,也不是一般首选的方法,但短向量可用于许多其他目的,故c(…)结构还是得以广泛的应用。2.4节将讨论读取数据的其他技术。现在,我们继续使用这一简单的方法。
你可以像对普通的数字一样对向量进行运算,只要它们有相同的长度即可。假设我们还有对应于上述体重的身高数据。一个人的体重指数(BMI)定义为体重(以kg为单位)除以身高(以m为单位)的平方。可以如下计算:

注意到该操作是按逐个元素的方式进行的(也就是说,BMI的第一个元素是60/1.752,以此类推),^运算符表示将一个值放到指数的位置上(在某些键盘上,^是一个“死键”,你可以通过按空格键之后使其显示)。
事实上,对不同长度的向量进行算术运算也是可能的。我们已经进行了这种计算,如在上面height^2的计算中,2就是1维的。在这种情况下,较短的向量被循环使用了。这通常发生于长度为1的向量(标量),有时也会发生在其他情形下,比如在需要一个循环计算模式的时候。如果较长的向量不是较短向量的倍数的话,将会出现警告。
这些向量化计算的约定使得一些特殊的统计计算变得容易。比如,考虑上述weight变量的均值和标准差计算。
首先,计算均值,:


然后把均值保存在变量xbar中,继续计算 。我们逐一观察每个部分的结果,各个偏差是

注意长度为1的xbar被循环使用,被weight中的每一个元素减掉。偏差的平方是

由于该命令与之前的一个很相似,因此通过编辑之前的命令来进行输入就会很方便。在大多数运行R的系统中,之前的命令可以通过向上箭头键调出。
偏差平方和可以由下式得到:

最后可以得到标准差为

当然,由于R是一个统计计算环境,这种计算过程已经有现成的,你只需要输入下述命令就可以得到同样的结果:

下面给出一个R做稍微复杂分析的例子,考虑以下内容:根据经验,一个正常体重的人的体重指数在20~25,我们想知道的是数据是否系统地偏离了它。假设有来自于一个正态分布的6个人的体重指数,你可以使用单样本t检验方法来检验它们是否具有假设的均值22.5。为此,你可以使用命令t.test。(你或许不知道t检验的理论,这里的例子目的在于给读者一个大致的印象,什么是“真正的”统计输出。t检验的完整介绍将在第5章给出。)


参数mu=22.5对一个形式参数mu赋值,其中的mu代表希腊字母__,通常用来表示理论均值。如果这里没有给定该值,t.test将默认mu=0,当然,这不是我们现在所关心的。
对于这样的检验,我们得到了比之前的例子更多的输出结果。输出的细节将在第5章解释,但是你可能关注p值,它用于对假设均值是22.5的检验。p值不小,意味着如果均值确实等于22.5的话,那么得到那些观测数据不是不可能的。(一般来说,实际的p值是计算得到大于0.344 9或小于0.344 9的t值的概率。)然而,你也可以看到真实均值的95%置信区间。区间很宽,意味着我们得到的关于真实均值的信息其实很少。
1.5 作图表达和分析数据的最重要的方面之一是生成适当的图形。类似于之前的S,R有一个构建图形的模型,可以进行简单的标准图形生成以及图形组件的精细控制。
如果你想研究weight和height之间的关系,第一想法就应是作图。命令如下:

执行后将得到如图1.2所示的结果。
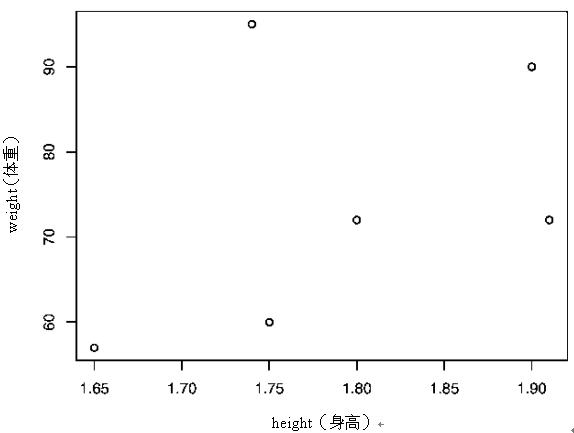
通常你会希望用不同的方式修改图像。为此目的,有很多作图参数供你设置。比如,我们试着使用关键字pch(绘图符号)改变绘图符号:
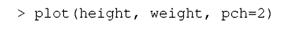
得到如图1.3所示形式,其中的点用三角符号标出。
BMI计算的思想是这个值应该独立于人的身高,从而给出一个数字表明这个人是否超重以及超重多少。由于一个正常的BMI值应该是22.5,故可以估计weight ≈ 22.5×height2。因此,你可以在图中叠加一个基于BMI为22.5的体重估计的曲线:

得到如图1.4所示的形式。函数lines将通过一条直线将(x,y)值增加到现有的图中。
对height定义一个新的变量(hh)而不是使用原来的height变量的原因有两个。首先,height和weight之间的关系是二次的,而非线性,虽然这一点从图上很难看出来。由于我们采用逐段的直线来近似一条曲线,因此用沿着x轴均匀分散的点比依赖于原始数据点的分散状态要好。第二,由于没有对height值排序,线段不会自动连接相邻的点,而是会在相隔很远的点间来回连接。














