1. 多边形内角和为(n-2)180º
证明:
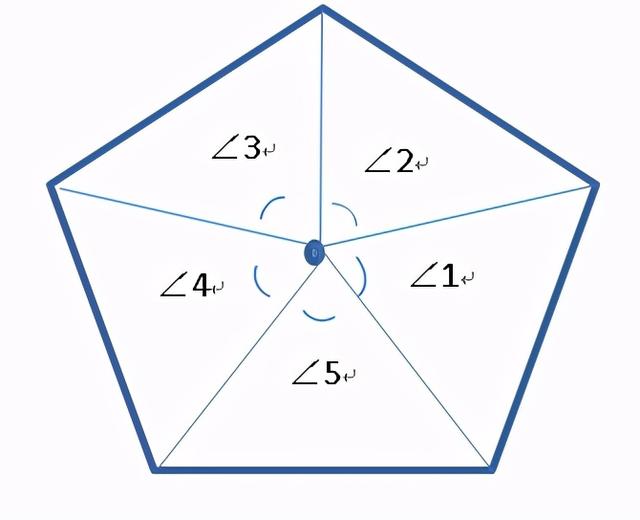
上图n边形,在中心找一点,连接中心和各个顶点,把五边形分成五n个三角形,求多边形的内角和转化为求三角形内角和问题。
n边形内角和=(180º-∠1) (180º-∠2) (180º-∠3) (180º-∠4) (180º-∠5) …..(180º-∠n)
=n*180º-(∠1 ∠2 ∠3 ∠4 ∠5 ……∠n)
=n*180º-360º
=180º(n-2)
2. 多边形的外角和为360º

证明:
因为:
180º-∠1 180º-∠2 180º-∠3 180º-∠4 180º-∠5 ……180º-∠n=(n-2)*180º
n*180º-(∠1 ∠2 ∠3 ∠4 ∠5 ……∠n)=(n-2)180º
n边形的外角和=∠1 ∠2 ∠3 ∠4 ∠5 ……∠n
所以 :
n*180-n边形的外角和=(n-2)180º
n边形的外角和= n*180º-(n-2)180º-=n*180º- n*180º 360º =360º
3. 多边形的对角线
(1) 对角线定义
连接多边形不相邻的两个顶点的线段叫做多边形的对角线
(2) n边形的一个顶点可以引出n-3条对角线,这些对角线可将n边形分成n-2个三角形

证明:
n边形共有n个顶点,因此剩余n-1个顶点,根据对对角线的定义,有两个顶点与这个顶点相邻,因此剩余顶点个数为(n-1)-2=n-3,从某一顶点只能向n-3个点引出n-3条对角线。
(1) n边形共有n(n-3)/2条对角线
证明:
根据(2)的结论,n边形每一个顶点有n-3条对角线,那么n边形共有n(n-3)条对角线,因为每一条对角线重复的计算了两次,因此对角线数为n(n-3)/2
4. 正多边形
(1) 定义在同以平面内各内角都相等,各边也相等的多边形叫做正多边形
(2) 正五边形1) 正五边形每个内角为3*180º/5=108º
2) 外角为:360º/5=72º
或者:180º-108º=72º
3) 共有n(n-3)/2=5(5-3)/2=5条对角线
(3) 正六边形
1) 正六边形每个内角为4*180º/6=120º
正六边形外对角线的交点是外接圆的圆心,把正六边形分成六个等边三角形
2) 外角为:360º/6=60º
或者:180º-120º=60º
3) 共有n(n-3)/2=6(6-3)/2=9条对角线
二、基础题型1. 例题1
正六边形的边长为3,较长的一条对角线长为?
根据上面正六边形的性质可知,较长的一条对角线为6
2. 考察知识点:(1) 等边三角形及内角为60º
(2) 正六边形
(3) 多边形的对角线
3. 解题思路和技巧利用正六边形的特点以及对角线的知识即可
三、综合题型

1) 解①:
因为;
正五边形每个内角大小为108º
AE=AB, AE=ED
所以:∠ABE=∠EAD=36º
因为:
∠BAD=∠EAB-∠EAD=108º-36º=72º
∠AME=∠ABE ∠BAD
所以:
∠AME=36º 72º=108º
所以①结论正确
2) 解②:
因为:
∠AEM=∠AED=108º
∠EAM=∠EAD=36º
所以:
ΔAME∽ΔAED
所以有:
AE/AD=AM/AE
又因为:
∠AED=108º
∠AEB=∠DEC=36º
∠AEN=∠AED-∠DEC=108º-36º=72º
∠AEN=72º
又因为
∠DNE=∠AME=108º
所以:
∠ANE=180º-∠DNE=180º-108º=72º
所以有:
∠AEN=∠ANE
AN=AE
因为:AE/AD=AM/AE AN=AE
所以:AN/AD=AM/AN
因此结论②正确


1) 正多边形
2) 等腰三角形
3) 直角三角形及勾股定理
4) 三角形全等
5) 三角形相似
(2) 解题思路和技巧①,利用正多边形的内角和、等腰三角形,三角形的一个外角和等于不相邻的两个内角和
②,根据公式AN/AD=AM/AN得出与AM和AD有关,找出ΔAME∽ΔAED,然后再找出AE=AN即可,利用角度关系很容易找出AE=AN
③,充分利用②的条件,根据公式AN/AD=AM/AN,列出方程就可以解决问题
④,利用全等、等腰三角形求出ΔEBC的高,就求出了他的面积。
,