小学奥数约数个数定理（小学奥数余数的三大定理）

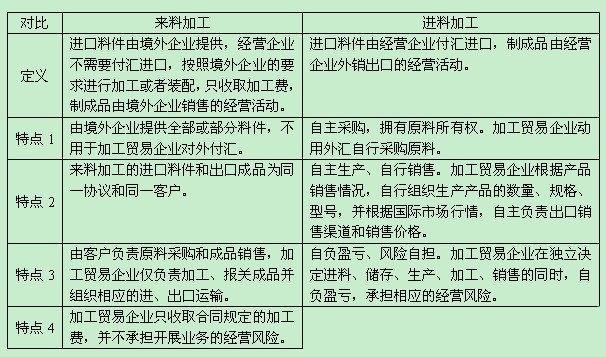
定理

对于一个大于1正整数n可以分解质因数：

则n的正约数的个数就是

。

其中a1、a2、a3…ak是p1、p2、p3，…pk的指数。

约数个数定理可以计算出一个数约数的个数，在小学奥数与中学竞赛中大有用处。

对于一个大于1正整数n可以分解质因数:n=p1^a1*p2^a2*p3^a3*…*pk^ak,

则由约数个数定理可知n的正约数有(a₁+1)(a₂+1)(a₃+1)…(ak+1)个，

那么n的(a₁+1)(a₂+1)(a₃+1)…(ak+1)个正约数的和为

f(n)=(p1^0+p1^1+p1^2+…p1^a1)(p2^0+p2^1+p2^2+…p2^a2)…(pk^0+pk^1+pk^2+…pk^ak)